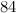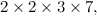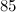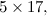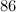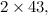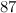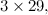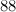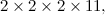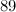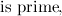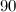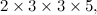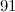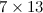Pagina 11
Numero e sistemi numerici
«Lo spirito matematico è patrimonio primordiale dell’umanità; esso si manifesta ovunque vivano esseri umani o laddove esistano ancora prove materiali di vita passata.»
Così scrive Willi Hartner in uno studio fondamentale su numeri e sistemi numerici, nel quale, a sostegno dell’esattezza della frase appena citata, si rifà alle opere d’arte degli uomini dell’età della pietra: «L’artista dell’età della pietra non ‘conta’ e non sa nulla dei rapporti matematici, ma obbedisce esclusivamente a un profondo istinto matematico In seguito, mediante l’astrazione, tale istinto viene imprigionato in forme geometriche e nel corso del tempo aiuta l’uomo a sviluppare concetti numerici e numeri, a ordinare le svariate apparizioni spazio-temporali in base a un ‘numero’ astratto. Ora, come scrive Karl Menninger nel suo libro, una multicolore varietà d’espressione si dispiega dinnanzi a noi, abituati a vedere e a comprendere tutto in base al nostro vecchio sistema decimale e ai numeri ‘arabi’ (già il passaggio al sistema di misura anglosassone presenta qualche difficoltà). Eppure, i sistemi numerici si basano su ritmi diversi, un esempio è costituito dal sistema binario che viene utilizzato dall’informatica e che già Leibniz nel 1697 aveva sviluppato nei suoi elementi fondamentali. Anche se il sistema decimale sembra essere il più diffuso, bisogna riconoscere ad altri la stessa importanza, soprattutto al sistema sessagesimale degli antichi Babilonesi, i quali oltre all’unità dieci conoscevano un’unità superiore, sessanta; le tracce di questo sistema sopravvivono ancora nei 360° del cerchio e nella suddivisione delle ore in minuti e secondi.
In molti casi, sistemi di calcolo e cifre possono essere derivati dalla semplice rappresentazione delle cinque o dieci dita; la forma dei numeri romani, che si richiama alle dita della mano, fa ripensare alla loro origine. Eppure, anche qui, il salto dopo il quattro, ovvero l’esclusione del pollice, rivela l’esistenza di un’altra possibilità di calcolo: dopo il quattro inizia un nuovo capitolo. D’altro canto, per formare una base di calcolo, venivano utilizzate non soltanto le dita delle mani, ma anche quelle dei piedi: nell’Europa occidentale e settentrionale, Celti, Baschi e altri popoli ricorrevano probabilmente a un sistema basato sul venti, come dimostra ancora oggi l’espressione francese quatrevingt (4×20) per dire ottanta. Anche l’inglese score (venti, ventina) richiama alla mente un’antica suddivisione basata sul venti.
Da non confondere con questo fondamentale metodo di conto sulle dita è la tecnica, anticamente assai sviluppata, che consentiva di contare fino a cento con l’ausilio delle dita: le unità e le decine venivano formate con le dita della mano sinistra, le centinaia con la mano destra. Gli stessi esegeti medievali della Bibbia, in particolare Beda il Venerabile, hanno fatto riferimento nelle loro interpretazioni a questi diffusi metodi di conto da loro considerati assai validi: pollice e indice della mano destra, uniti a formare un cerchio, significavano cento e in un certo senso diventavano simbolo dell’eternità racchiusa su se stessa. I venditori orientali sono tuttora insuperabili in questo sistema di conto basato sulle dita; spesso utilizzano anche l’abaco, un antico pallottoliere, e con l’ausilio di questo strumento sono in grado di eseguire con estrema rapidità le più complesse operazioni di calcolo, come facevano anche i mercanti europei del Medioevo.
Ogni cultura aveva i propri segni numerici tipici, si pensi ai quipus degli Inca (corde di diversi colori a cui venivano fatti dei nodi ad altezza variabile) o all’espressione «far la tacca sul legno», che ricorda l’abitudine di segnare i debiti incidendo dei tagli profondi su un pezzo di legno. Vi sono i numeri egizi figurati, quelli fenici e quelli romani, in proporzione ancora primitivi; le operazioni di calcolo più complesse venivano facilitate equiparando lettere e numeri, come avveniva anticamente in Grecia e come avviene ancora oggi presso Ebrei e Arabi. Ogni lettera dell’alfabeto ha un valore numerico (l’alfabeto arabo viene ancora ordinato in base alla sequenza delle lettere dell’antico alfabeto semita) e da questo duplice significato è possibile ottenere facilmente delle corrispondenze tra nomi, vocaboli e numeri: il numero seicentosessantasei contenuto nell’ Apocalisse e le sue molteplici soluzioni sono un esempio di quest’arte, che raggiunse il suo massimo sviluppo nella cabala ebraica e nella tradizione islamica. Per esempio si possono utilizzare dei versi molto significativi per stabilire una data: il valore numerico del titolo Bagh u bahar (Giardino e primavera) sta a indicare che questa gradevole opera venne scritta nell’anno 1216 del calendario islamico ovvero il 1801-2 della nostra era. Con una parola o un verso adeguati è possibile indicare la data di morte di un noto personaggio oppure caratterizzare in modo preciso il defunto.
Nella classificazione di Hartner questi poliedrici numeri cifrati, ampiamente diffusi nel campo della mistica e delle arti magiche, sono preceduti dai numeri cinesi, i quali a loro volta sono preceduti dal sistema cifrato sumero-babilonese, già allora molto elaborato: non bisogna dimenticare del resto che la terra racchiusa tra i due corsi d’acqua fu anche la patria dell’astronomia e della matematica e che molti dei significati ‘religiosi’ tutt’oggi validi traggono origine da questa civiltà. Sempre secondo Hartner, il sistema cifrato più sofisticato è quello dei Maya, i quali seppero elaborare una teoria astronomica di stupefacente esattezza: il loro antichissimo calendario, basato sulle sessantacinque rivoluzioni sinodiche di Venere, è più preciso di qualsiasi altro calendario. Infine, vengono i nostri numeri arabi, o per meglio dire indiani: l’origine indiana di questi numeri è tuttora riconoscibile dal fatto che non vengono scritti da destra a sinistra come l’alfabeto arabo bensì, anche dagli Arabi, da sinistra a destra.
Questi numeri. adottati dagli Arabi non molto tempo dopo la nascita dell’islam, sono particolarmente caratterizzati dall’uso dello zero, che facilita anche le complesse operazioni di calcolo. Fonti indiane citano questo numero, schunya (il vuoto) al più tardi nel VI secolo d.C.; le nove cifre indiane vengono menzionate per la prima volta in un testo siriano del 662. Molto tempo prima che l’Occidente venisse a conoscenza dei pratici numeri arabi, i dotti Arabi concepirono opere matematiche. All’opera di Muhammad ibn Musa al-Khwarizmi, Hisab al-dschabrh wa’l muqabala (Il libro dell’integrazione e dell’equilibrio), scritta poco dopo l’anno 800 e tradotta in latino da Robert da Chester nel XII secolo, siamo debitori non soltanto del concetto di ‘algebra’ (da aldschabr o al-gabr), ma anche di quello di ‘algoritmo’, dal complesso nome dell’autore. Lentamente, i numeri arabi si diffusero anche in Europa occidentale, soprattutto grazie all’opera di studiosi come Leonardo Fibonacci di Pisa (morto nel 1250) e Giovanni di Sacrobosco, che fecero conoscere i nuovi numeri e le operazioni di calcolo. Intorno al 1240, un francescano francese, Alessandro de Villa Dei compose un Carmen de Algorismo, un poema di 244 versi dedicato al nuovo metodo di calcolo che, come egli credeva, era stato inventato dal re indiano Algor (Karl Menninger).
Lo zero, che i più antichi sistemi di calcolo non conoscevano, generò dapprima molta confusione, come rivela anche la sua storia linguistica: dal nome arabo sifr, nacque da un lato cifra, chiffre e Ziffer e dall’altro zero. Lo zero, che significa nulla, ma che dà valore al numero che lo segue o lo precede, nel XV secolo meritava l’appellativo di umbre et encombre (oscuro e non chiaro); il vocabolo tedesco Null deriva da nulla figura (nessun segno). Bisogna tuttavia sottolineare che, in maniera del tutto autonoma rispetto all’invenzione indiana dello zero (e ovviamente alcuni secoli prima), i Maya, e forse già gli 0lmechi, conoscevano lo zero, che nel loro sistema basato sul venti seguiva il diciannove. La scrittura di questo sistema si basava su una combinazione di punti e linee oppure di geroglifici a forma di testa in diverse varianti.
Per quanto pochi numeri e sistemi numerici si somigliassero, è lecito supporre che tutte le culture si ponessero di fronte alle operazioni di calcolo con il medesimo atteggiamento.
F.C. Endres racconta di quando, agli inizi del XX secolo, volle fare un esperimento matematico in uno sperduto villaggio turco: «Misi alcune mele per terra e chiesi a un ragazzo di contarle. Nonostante fosse in grado di aiutarsi con le dita, non riusciva ad andare oltre il cinque. Tra il cinque e il dieci sbagliava spesso; se poi mettevo per terra più di dieci mele e gli dicevo di contarle, si limitava a dire che erano molte, senza tuttavia riuscire a dire un numero preciso…» Quando si trattò di contare i sassolini che Endres gettava in acqua, il ragazzo arrivò soltanto al tre o al quattro. Per contare nello spazio, poteva sempre servirsi delle dita e vedere ciò che gli stava dinnanzi, ma contare nel tempo era assai più complicato, in quanto bisogna scoprire con quale frequenza eventi identici o simili si ripetono. Sembra che una duplice o triplice ripetizione di urla, suoni, battute sia alquanto comune, mentre altri raggruppamenti e sequenze ci paiono perlomeno difficili. Se si cerca di contare o di completare i complicati ritmi di una musica armena o indiana, si scoprirà che presto si perde il tempo e non si riesce più a contare.
Non si possono quindi sottovalutare altre culture solo perché si avvalgono di sistemi di calcolo diversi dal nostro: anche se alcune tribù africane non sanno quasi ‘contare’ come lo intendiamo noi, hanno la capacità per noi inspiegabile di comprendere quantità precise, anche molto vaste e di accorgersi subito se per esempio manca un capo di bestiame dal loro gregge.
In molte culture, i numerali variano a seconda di ciò che viene contato: vi sono concetti diversi per dire «sei lunghe cose», «sei mucche», oppure «sei uomini». Classificazioni di questo genere esistono ovunque; i Papua distinguono fino a venti diversi gruppi di numerali riferiti a oggetti specifici. Tuttavia, anche nelle culture superiori rimangono tracce di simili metodi di calcolo: si misura, o si misurava, la lunghezza della stoffa in ‘cubiti’, l’altezza in ‘piedi’, la profondità in ‘tese’ oppure, se si trattava di acqua in ‘bracci’ (in inglese fathom), la velocità in acqua in ‘nodi’. Per gli animali si usano termini collettivi diversi a seconda del genere: una ‘muta’ di cani, un ‘branco’ di lupi, una ‘mandria’ di mucche, un ‘gregge’ di pecore. Soprattutto nel linguaggio dei cacciatori tali espressioni sono ancora d’uso comune, come dimostra il divertente libretto inglese An Exaltation of Larks (Esaltazione delle allodole). Anche la lingua parlata conserva alcuni concetti numerici speciali: per esempio l’esercito è diviso in ‘battaglioni’, ‘compagnie’, ‘squadroni’ e così via, parole che hanno un preciso valore numerico.
In tutto ciò non vi è nulla di mistico o di magico, eppure già presso i popoli più antichi si ha la netta sensazione che i numeri siano una realtà, che siano circondati da un campo di forze attivo, come ha constatato Lévy-Bruhl. Il numero non è forse, come dicevano egli antichi Indiani, «simile a Brahma», cioè simile al divino? In certi antichi testi indiani vengono rivolte delle regolari invocazioni: «Lode all’Uno! Lode al Due!… Lode al Cento!» e così via. Tali sentimenti rispetto al numero si sono tramandati e lo stesso nostro sistema di calcolo, apparentemente così sobrio e imparziale, che possiamo ricondurre alle dieci dita, alle quattro fasi lunari e ai dodici mesi solari, ha avuto in passato risvolti anche misteriosi, che hanno portato ad attribuire ai numeri particolari forze segrete, a utilizzarli per formulare giuramenti magici e soprattutto per fare previsioni astrologiche. Anche le grandi religioni superiori del mondo conoscono l’uso mistico e religioso dei numeri fino ai giorni nostri. Nelle arti magiche, in cui l’esecutore cerca di influenzare gli avvenimenti a proprio vantaggio o a svantaggio di un terzo mediante l’impiego di determinate formule, l’uso dei numeri ha un ruolo di grande potenza, in quanto ogni numero viene visto nel proprio ‘campo di forze’, nei suoi nessi cosmici, e il ricorso al numero giusto o all’esatto numero di ripetizioni delle formule o dei giuramenti, delle purificazioni o delle rivoluzioni è considerato decisivo per la riuscita del procedimento magico.
Pagina 31
Numeri e superstizione
Naturalmente, non sempre l’antica fede nell’ordine dei numeri portava a scoperte scientifiche; molto più spesso, il numero veniva utilizzato per scopi magici e la fede in tali manipolazioni si è conservata sino ai giorni nostri e forse si è addirittura rafforzata a livello popolare. Nella primavera del 1984 mi capitò sotto mano un pieghevole americano totalmente dedicato alla numerologia, alle vibrazioni numeriche, alla scoperta dei numeri fortunati e così via. Si tratta di pratiche che, seppure di origine molto antica, non hanno perso nulla del loro fascino. Il libro di E.T. Bell Numerology (Numerologia) rappresenta il più netto rifiuto di tali credenze superstiziose, contro le quali si è sempre pronunciato anche Endres. Tutto, infatti, può essere manipolato: ogni nome e ogni data, abilmente scomposti e quindi ricomposti, soprattutto mediante la somma delle cifre, possono condurre al risultato desiderato. È bene ricordare i risultati raggiunti ‘in modo scientifico’, come per esempio i libri di Oskar Fischer, pubblicati verso la fine della prima guerra mondiale, e in particolare Auferstehungsboffnung in Zahlen (La speranza di risurrezione dei numeri). Questi testi tentavano di interpretare con mezzi statistici determinate costellazioni numeriche contenute nell’Antico Testamento e di trarne delle possibili chiavi interpretative della storia di Israele e del primo cristianesimo. Si pensi ancora all’affascinante libro di McClains, nel quale l’autore tenta, con l’ausilio della speculazione numerica, la ricostruzione del mitico monte cosmico e del suo rapporto con la Kaaba alla Mecca e, al di là della simbologia numerica, fa alcune interessanti osservazioni su certi fenomeni riscontrabili nell’islam; oppure si pensi all’esperimento condotto da un pio musulmano che cercò di dimostrare, servendosi di un computer, che il Corano è fondato unicamente ed essenzialmente sul numero diciannove…
Tali tentativi di ordinare numericamente fatti storici e mistici non influenzano il piacere del tutto naturale per l’armonia dei numeri e, per taluni individui, anche la sensazione profondamente radicata che nella loro esistenza s1 ripetano certe costellazioni numeriche. C’è una zona limite in cui la tradizione da un lato e la psicologia dall’altro svolgono un ruolo importante; eppure siamo ancora scarsamente consapevoli di come gran parte dei nostri gesti quotidiani o delle nostre espressioni siano caratterizzati da un ritmo numerico, in cui predomina soprattutto il tre, riscontrabile persino in alcune piccole banalità della nostra vita di tutti i giorni, per esempio le tre luci del semaforo o il triplice «Urrà!» che si lancia durante i festeggiamenti. Certi numeri sono sempre stati adoperati per conferire a una data opera letteraria una certa atmosfera; spesso alcuni termini e alcune espressioni sono scaturite inconsciamente dalla penna del poeta (persino dello scienziato) quando per esempio procede a passi triadici o a quartine, oppure quando attribuisce una determinata suddivisione metrica al contenuto del suo verso, quando crea una ‘trilogia della passione’ o quando, come nel mondo islamico, compone le sue odi romantiche in quintetti. Lo stesso vale per l’artista, quando per esempio cerca di avvicinarsi il più possibile alla sezione aurea. Si tratta di strutture inconsce, che consentono a interpreti successivi di pensare a una intenzionale mistica numerica che magari lo stesso autore ignorava.
Dovremmo forse biasimare i pitagorici per aver attribuito all’elemento femminile i numeri pari, quando la biologia ci dimostra che la forma genetica del maschile è xy, mentre quella del femminile è xx, ossia un numero pari?
Pagina 32
Giochi numerici e quadrati magici
Esistono un’infinità di giochi basati sui numeri, alcuni dei quali molto divertenti, che tuttavia sono puramente aritmetici e solo di rado trovano un impiego in campo magico o mistico. Molti di essi hanno un proprio fascino; il nove, per esempio, ha un ruolo del tutto particolare. Già in passato i matematici si erano accorti che tutti i prodotti di nove danno come somma ancora nove (4×9=36, 3+6=9; 7×9=63, 6+3=9); si era inoltre constatato che cinque e sei, elevati a potenza, finiscono sempre per cinque oppure per sei: 5^2=25, 5^3=125 e così via. Moltiplicando certi numeri, si ottengono delle interessanti scale numeriche:
1 x 9 + 2 = 11
12 x 9 + 3 = 111
123 x 9 + 4 = 1.111
1.234 x 9 + 5 = 11.111
12.345 x 9 + 6 = 111.111
123.456 x 9 + 7 = 1.111.111
1.234.567 x 9 + 8 = 11.111.111
12.345.678 x 9 + 9 = 111.111.111
123.456.789 x 9 +10 = 1.111.111.111
Se si inizia con 1×8+1=9 e si prosegue con le righe successive trattandole come nel primo esempio, si ottiene una scala ancora più sorprendente. L’ultima riga apparirà infatti come segue:
123.456.789 x 8 + 9 = 987.654.321
E non è forse stupefacente che, moltiplicando il numero 142.857 per 2, 3, 4 oppure 6, si ottenga come risultato un numero che è sempre composto dalle stesse cifre, anche se in diversa successione?
Pagina 52
Die Zwei ist Zwillingsfrucht am Zwige;
süß und bitter.
(Il due è dubbio, dissidio, è discordia, divisione, ermafrodito,
il due è frutto gemello sul ramo;
dolce e amaro.)
Così dice Rückert con un geniale gioco di parole in Weisheit der Brahmanen (Saggezza dei brahmani), e allude con ciò a molti dei lati ‘negativi’ di questo numero. Quindi il due è il crollo dell’assoluta unità divina; è il numero legato al mondo delle creature «in quanto la creatura è di per sé duplice», come dice Weigel.
In ogni aspetto della vita emerge la posizione centrale di tale contrasto (che tuttavia non deve essere necessariamente negativo): già la possibilità di dialogare, di rivolgersi a un interlocutore incarna la tensione tra l’ Io e il Tu, che può essere feconda, ma anche distruttiva.
La linea, simbolo geometrico dei due, separa e unisce. È interessante notare che molte lingue conoscono il duale, le cui particolarità erano già state descritte da Wilhelm von Humboldt nel 1828. Questo duale, che esprime il rapporto tra due esseri, ma non tra l’Io e il molteplice, è riscontrabile in numerose lingue antiche: se ne conservano tracce in certi dialetti tedeschi, come in quello della Vestfalia, dell Austria e dell’alta Baviera. In particolare, alcuni residui di duale sono tuttora riconoscibili nei pronomi personali, come si osserva nelle lingue slave. Anche nell’arabo il duale è perfettamente conservato.
Tale contrapposizione tra Io e Tu reca in sé anche il contrario, e tale contrasto diviene particolarmente evidente quando l’Io umano si considera di fronte al Tu di un Dio ritenuto assolutamente Uno, poiché non è concepibile alcuna opposizione a questo Uno. Così, naturalmente, il due diviene il numero della contraddizione, del non-divino, e in quanto numero della discordia viene impiegato scarsamente anche in magia.
Non si può pensare in questo caso all’equazione matematica 1+1=2, in quanto da un punto di vista esoterico e mistico esiste solo l’Uno, l’Irripetibile. Un dio e un altro dio sono due divinità, che non corrispondono più all’ideale dell’Eterno Uno. Per questa ragione, nel linguaggio religioso e magico, il due è sempre simbolo della contrapposizione di due unità non divine, bensì relative.
Di nuovo Agrippa di Nettesheim ci offre un’efficace descrizione delle qualità magico-mistiche del due: esso è «il numero dell’uomo che viene chiamato ‘altro’ e il numero del mondo inferiore».
Il due è il numero del genere sessuale e del male (poiché, come sottolineano tutti gli esegeti medievali, nella storia della creazione al secondo giorno manca la formula ‘ed esso fu buono’).
Anche gli spiriti malvagi, che opprimono i viandanti, devono sottostare al due. Il fatto che, nelle lingue scandinave, ‘il secondo’ si dica andra ben si addice alla formulazione di Agrippa, che naturalmente contrappone l’uomo come ‘altro’ Dio.
Il due è un numero che ha origine con la creazione, poiché senza la polarità che esso esprime, la vita non potrebbe esistere. Come la corrente elettrica ha bisogno di un polo positivo e di uno negativo, come la vita è ritmata dall’inspirazione e dall’espirazione, dalla sistole e dalla diastole del battito cardiaco, così il due è legato a tutte le manifestazioni umane.
Goethe, che conosceva assai bene il segreto della polarità, dice ispirandosi allo stile islamico:
Im Atemholen sind zweirlei Gnaden... Du danke Gott, wenn er dich preßt Und danke ihm, wenn er dich wieder entläßt. (Nel respiro che trattieni vi è una duplice grazia... Ringrazia Dio, quando Egli ti preme E ringrazialo, quando Egli di nuovo ti lascia.)
Nel suo libro Das Heilige (Il sacro), Rudolf Otto spiega che Dio si manifesta come mysterium tremendum e come mysterium fascinans, come la tradizione islamica sa da tempo: Dio mostra la sua bellezza (dschamal) e la sua maestà (dschalal), la sua benevolenza e la sua ira, che indicano la sua ineguagliabile, irraggiungibile perfezione.
La mistica islamica, similmente alla cabalistica, attribuisce alla seconda lettera dell’alfabeto, b, il valore numerico due, in riferimento al mondo delle creature. E come la Bibbia comincia con la b di Be reschith («In principio…»), anche il Corano inizia con Bismillah (Nel nome di Dio…»): in entrambi i casi, il libro sacro viene rivelato al mondo mediante queste due lettere.
Un simbolo che esprime in modo particolarmente intenso questa dualità umana è quello scelto dal poeta mistico persiano Gialal al-Din Rumi. Egli paragona la parola creativa di Dio kun, «Sia!», (scritto kn) con una corda a doppio filo (ossia un ‘refe’ nel senso più vero del termine), che appare in ogni manifestazione, ma che mostra a colui che sa il cammino verso la verità nascosto dietro il mondo dei contrasti.
La religione cinese ha trovato nel simbolo yin e yang un’efficace rappresentazione della polarità da cui scaturisce la vita: queste due forze sono simbolo dell’elemento attivo e dell’elemento passivo, maschile e femminile, fecondante e fecondato, del fuoco e dell’acqua.
Pagina 62
Il tre va oltre la contrapposizione del due, come è chiaramente espresso nella locuzione «tra i due litiganti il terzo gode».
Il segreto del tre è stato spesso cantato, per esempio nel XVI secolo dal poeta francese G. Du Bartas; il suo Semaine del 1587, tradotto in inglese da Joshua Sylvester, dice a proposito del tre:
The eldest of odds, God's Number properly... Heaven's dearest number, whose inclosed center Doth equally from both extremes extend, The first that hath a beginning, midst, and end. (I1 più vecchio dei numeri dispari, per l'esattezza il numero di Dio... Il numero più caro al paradiso, il cui centro racchiuso Si estende eguàlmente dai due estremi, Il primo che ha un inizio, un mezzo e una fine.)
Quando, nell’immediato dopoguerra, Wolfgang Philipp, teologo di Marburgo, presentò la sua prova scritta di libera docenza dal titolo ‘La trinità nel nostro essere’, intendeva riferirsi alla tendenza innata in ogni forma di vita alla tripartizione, che già Ernst Cassirer aveva trattato nella sua Filosofia delle forme simboliche del 1923: «Il problema dell’unità che si scompone, che diviene ‘altro e secondo’, per tornare infine a ricomporsi in una terza natura, appartiene all’intero patrimonio spirituale dell’umanità. Se dapprima esso si manifesta, in questa concezione puramente intellettuale, nella storia speculativa delle religioni, tuttavia la diffusione generale dell’idea del Dio ‘uno e trino’ dimostra che tale idea deve avere un concreto fondamento emotivo, al quale essa si rifà e dal quale rinasce sempre nuova».
Tuttavia Wolfgang Philipp, per il quale ogni esistenza è basata su un’emozione tripolare e si manifesta in forma di onda, radiazione e condensazione, afferma: «Poiché, conformemente all’esistenza, siamo fatti in modo tripolare, tendiamo esistenzialmente a tutto ciò che è trino; perciò le triadi sono ‘buone cose’ e noi stessi siamo buone cose, quando in esse troviamo compiuta e suggellata in modo attivo-mediale-passivo la nostra legge».
Da un punto meramente linguistico, la differenza tra le azioni compiute da due persone e quelle compiute da più persone viene sottolineata rispettivamente attraverso l’uso del duale e del plurale.
In un interessante saggio del 1903, Raimund Müller cercò di spiegare l’importanza del tre nella leggenda, nella poesia e nell’arte, rilevando come la triade emerga dalla semplice osservazione della natura: l’uomo vide l’acqua, l’aria e la terra, la cui conoscenza si eleva poi nella concezione di tre mondi (i germanici Midgard, Asgard e Niflheim); poi scoprì tre stati di aggregazione (solido, fluido, gassoso), distinse in tre gruppi le cose create (minerali, vegetali, animali) e osservò che le piante avevano radice, stelo e corolla, come il frutto aveva buccia, polpa e nocciolo; il corso del sole gli apparve diviso in mattino, mezzogiorno e sera. Ogni esperienza si svolgeva nell’ambito delle coordinate spaziali di altezza, lunghezza e profondità; il mondo della nostra percezione sensoriale è tridimensionale. La vita stessa è suddivisa in divenire, essere e perire; un tutto perfetto è formato da tesi, antitesi e sintesi. Infine, basta pensare ai tre colori fondamentali, rosso, giallo e blu, miscelando i quali si ottiene l’intera gamma dei colori.
TecaLibri: Franz Carl Endres: Dizionario dei numeri
The Mystery of Numbers – cedarcitylodge.org
A whirlpool of numbers
by Nicholas Mee
Jeserac sat motionless within a whirlpool of numbers. The first thousand primes, expressed in the binary scale that had been used for all arithmetical operations since electronic computers were invented, marched in order before him. Endless ranks of 1’s and 0’s paraded past, bringing before Jeserac’s eyes the complete sequences of all those numbers that possessed no factors except themselves and unity. There was a mystery about the primes that had always fascinated Man, and they held his imagination still.Jeserac was no mathematician, though sometimes he liked to believe he was. All he could do was to search among the infinite array of primes for special relationships and rules which more talented men might incorporate in general laws. He could find how numbers behaved, but he could not explain why. It was his pleasure to hack his way through the arithmetical jungle and sometimes he discovered wonders that more skilful explorers had missed.
He set up the matrix of all possible integers, and started his computer stringing the primes across its surface as beads might be arranged at the intersections of a mesh. Jeserac had done this a hundred times before and it had never taught him anything. But he was fascinated by the way in which the numbers he was studying were scattered, apparently according to no laws, across the spectrum of the integers. He knew the laws of distribution that had already been discovered, but always hoped to discover more.
from The City and the Stars by Arthur C. Clarke (1956)
The building blocks of arithmetic
 Carl Friedrich Gauss
Carl Friedrich Gauss
In the words of the great German mathematician Carl Friedrich Gauss: “Mathematics is the Queen of the Sciences and Arithmetic is the Queen of Mathematics.” The modern name for the branch of mathematics that Gauss was referring to as Arithmetic is Number Theory – the study of the properties of the positive whole numbers or integers. The 19th century mathematician Kronecker famously claimed that “God made the integers, all the rest is the work of man.”
The fundamental building blocks of Number Theory are the primes. These are the numbers: 2, 3, 5, 7, 11, 13,… defined as the whole numbers that cannot be divided exactly by any other whole number, excluding the trivial division by the number 1. Primes cannot be broken down into simpler components; they play a role in mathematics that is similar to the role of the elements in chemistry. From the 100 or so chemical elements it is possible to synthesize the millions of compounds that are studied by chemists. The Fundamental Theorem of Arithmetic, which was proved by Euclid, states that
All positive whole numbers are either primes or they can be uniquely decomposed into a product of primes.
For instance:
If we take all the primes less than 300, we find that there are just 62 of them:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29,
31, 37, 41, 43, 47, 53, 59, 61, 67, 71
73, 79, 83, 89, 97, 101, 103, 107, 109, 113,
127, 131, 137, 139, 149, 151, 157, 163, 167, 173,
179, 181, 191, 193, 197, 199, 211, 223, 227, 229,
233, 239, 241, 251, 257, 263, 269, 271, 277, 281,
283, 293.
25 of these primes are below 100, 21 are between 100 and 200 and 16 are between 200 and 300. It looks as though the primes become more spread out as their size increases. If we look further we find that between 10,000 and 10,100 there are just 11 primes, between 100,000 and 100,100 there are just 6. This seems to confirm that the primes become rarer as they become bigger, but do they eventually die out altogether? We know that there are no naturally occurring elements on Earth beyond number 92 – Uranium. But is the same true of the primes? What is the biggest prime number?
There is no biggest prime
The properties of prime numbers have been studied by mathematicians since antiquity. It was the Ancient Greeks who first proved that there are infinitely many primes, so there is not, in fact, a biggest prime number. Euclid’s Elements provides the oldest known proof. The proof works by showing that if we assume that there is a biggest prime number, then there is a contradiction. We can number all the primes in ascending order, so that 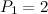 ,
, 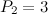 ,
, 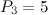 and so on. If we assume that there are just
and so on. If we assume that there are just 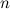 primes, then the biggest prime will be labelled
primes, then the biggest prime will be labelled 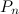 . Now we can form the number
. Now we can form the number 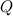 by multiplying together all these primes and adding 1, so
by multiplying together all these primes and adding 1, so
![\[ Q = (P_1 \times P_2 \times P_3 \times P_4... \times P_{n}) + 1. \]](http://plus.maths.org/MI/d29262594d0e85146ede2b8bfe25f3ac/images/img-0007.png) |
Now we can see that if we divide 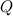 by any of our
by any of our 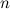 primes there is always a remainder of 1, so
primes there is always a remainder of 1, so 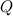 is not divisible by any of the primes. But we know that all positive integers are either primes or can be decomposed into a product of primes. This means that either
is not divisible by any of the primes. But we know that all positive integers are either primes or can be decomposed into a product of primes. This means that either 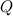 must be prime or
must be prime or 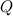 must be divisible by primes that are larger than
must be divisible by primes that are larger than 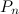 . Our assumption that
. Our assumption that 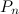 is the biggest prime has led us to a contradiction, this assumption must therefore be false, so there is no biggest prime.
is the biggest prime has led us to a contradiction, this assumption must therefore be false, so there is no biggest prime.
How are primes distributed?
We now know that the primes become sparser as they become bigger, but they don’t dwindle away completely. So the next question is, can we understand how the primes are distributed? Can the primes be fitted into a pattern in the way that the elements can be organised in the Periodic Table? This is one of the most important problems in the whole of mathematics.
The spacing between primes seems quite irregular, but there does appear to be a tendency for the spacing to increase, as we noted above. The Prime Number Theorem states that the function 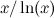 , where
, where 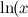 ) is the natural logarithm of
) is the natural logarithm of  , gives a reasonable approximation for the number of primes less than
, gives a reasonable approximation for the number of primes less than  , which we will represent as
, which we will represent as 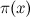 . As
. As  increases, this approximation becomes ever more accurate. The following table compares these two functions:
increases, this approximation becomes ever more accurate. The following table compares these two functions:
| x | Pi(x) | x/ln(x) | Pi(x)/(xln(x)) |
| 1000 | 168 | 145 | 1.159 |
| 10,000 | 1,229 | 1086 | 1.132 |
| 100,000 | 9,592 | 8,686 | 1.104 |
| 1,000,000 | 78,498 | 72,382 | 1.084 |
| 10,000,000 | 664,579 | 620,420 | 1.071 |
| 100,000,000 | 5,761,455 | 5,428,681 | 1.061 |
There is no simple formula that will generate all the primes, but Euler showed that the formula
![\[ f(n) = n^2 - n + 41 \]](http://plus.maths.org/MI/f84eca101f406a058ae2b5f5b913bdaa/images/img-0001.png) |
is remarkable because it is equal to a prime for every integer value of 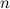 up to 40. The primes generated by the formula are:
up to 40. The primes generated by the formula are:
41, 43, 47, 53, 61, 71, 83, 97, 113, 131,
151, 173, 197, 223, 251, 281, 313, 347, 383, 421,
461, 503, 547, 593, 641, 691, 743, 797, 853, 911,
971, 1033, 1097, 1163, 1231, 1301, 1373, 1447, 1523, 1601.
The formula necessarily fails to produce a prime when 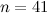 , because in this case
, because in this case 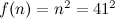 .
.
Euler also devised a much more important function that is now known as the zeta function:
![\[ \zeta (s) = \Sigma (1/n^ s) = 1^{-s} + 2^{-s} + 3^{-s} + 4^{-s} +... \]](http://plus.maths.org/MI/8aa46cefa0350756c36e81e2b2e2912c/images/img-0001.png) |
Euler showed that the zeta function is equal to an infinite product
![\[ z(s) = \Pi \frac{1}{(1 - 1/p^ s)} = \frac{1}{(1 - 1/2^ s)(1 - 1/3^ s)(1 - 1/5^ s)(1 - 1/7^ s)...}, \]](http://plus.maths.org/MI/8aa46cefa0350756c36e81e2b2e2912c/images/img-0002.png) |
where the product is over all the primes 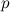 . This is a remarkable result: when the zeta function is expressed as the sum of an infinite number of terms, the sum includes a term that takes a value for every positive integer, but when expressed as an infinite product the only terms that are included are those that take a value for a prime.
. This is a remarkable result: when the zeta function is expressed as the sum of an infinite number of terms, the sum includes a term that takes a value for every positive integer, but when expressed as an infinite product the only terms that are included are those that take a value for a prime.
The zeta function, as defined by Euler, is only valid for values of  that are greater than 1. For these values of
that are greater than 1. For these values of  the zeta function can be summed to a finite value, even though the number of terms is infinite. However, if
the zeta function can be summed to a finite value, even though the number of terms is infinite. However, if  is equal to or less than 1, the series diverges, so the function is not well defined. For instance, taking
is equal to or less than 1, the series diverges, so the function is not well defined. For instance, taking 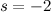 gives
gives
![\[ \Sigma (1/n^{-2}) = \Sigma n^2 = 1 + 4 + 9 + 16 + ..., \]](http://plus.maths.org/MI/8aa46cefa0350756c36e81e2b2e2912c/images/img-0006.png) |
a series which increases without end. By comparison, when 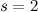 ,
,
![\[ \zeta (2) = \Sigma (1/n^2) = 1^{-2} + 2^{-2} + 3^{-2} + 4^{-2} + .... = 1 + 1/4 + 1/9 + 1/16 + .... \]](http://plus.maths.org/MI/8aa46cefa0350756c36e81e2b2e2912c/images/img-0008.png) |
This series can be summed to give 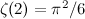 .
.
The Riemann Zeta Function
 Georg Friedrich Bernhard Riemann
Georg Friedrich Bernhard Riemann
In 1859 Georg Friedrich Bernhard Riemann published his only paper on Number Theory. In this paper Riemann found a function that is identical to Euler’s zeta function for values of  that are greater than 1, but that is well defined for all real numbers. The Riemann zeta function is actually defined for complex values of
that are greater than 1, but that is well defined for all real numbers. The Riemann zeta function is actually defined for complex values of  , where
, where 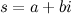 and
and 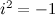 . Riemann proved that there were many deep connections between his analytically continued zeta function and the distribution of primes. Riemann’s intuition was quite remarkable in connecting the properties of a continuous function of a complex variable to the properties of the primes which are real and discrete. More specifically, Riemann showed that
. Riemann proved that there were many deep connections between his analytically continued zeta function and the distribution of primes. Riemann’s intuition was quite remarkable in connecting the properties of a continuous function of a complex variable to the properties of the primes which are real and discrete. More specifically, Riemann showed that 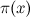 , the number of primes less than
, the number of primes less than  , is related to the points at which the zeta function is equal to zero – these points are known as the zeroes of the function. Riemann found that when
, is related to the points at which the zeta function is equal to zero – these points are known as the zeroes of the function. Riemann found that when  is a real number the zeta function only equals zero when
is a real number the zeta function only equals zero when  is equal to a negative even integer, that is at the points
is equal to a negative even integer, that is at the points  But Riemann also found other zeroes of the zeta function, all of which appeared to be on the line
But Riemann also found other zeroes of the zeta function, all of which appeared to be on the line 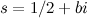 . The approximate value for the first of these is at
. The approximate value for the first of these is at 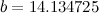 . Riemann conjectured that all the non-real zeroes of the zeta function lie on the line
. Riemann conjectured that all the non-real zeroes of the zeta function lie on the line 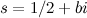 , although he was unable to prove this. The conjecture has become known as the Riemann Hypothesis and it is the key to understanding the distribution of the primes. Recent computer-based calculations have shown that at least the first 100 billion zeroes, with non-real
, although he was unable to prove this. The conjecture has become known as the Riemann Hypothesis and it is the key to understanding the distribution of the primes. Recent computer-based calculations have shown that at least the first 100 billion zeroes, with non-real  , all fall on Riemann’s line. But, as yet, there is still no proof that there are no exceptions to this pattern.
, all fall on Riemann’s line. But, as yet, there is still no proof that there are no exceptions to this pattern.
The British number theorist G.H. Hardy relates in his book “A mathematician’s apology” that before setting out on his return voyage over the North Sea from Denmark in the 1920s, expecting the crossing to be treacherous, he posted a note to a colleague to say that he had proved the Riemann Hypothesis. Although a staunch and proselytizing atheist, Hardy explained that he had sent the note in order to guarantee that God would not allow him to drown. Because if he had drowned that would mean that proofs had been claimed for both of the two most famous problems in mathematics: Fermat’s Last Theorem and the Riemann Hypothesis, but that the mathematician making the claim had died before communicating the proof to anyone else. Fermat’s Last Theorem had achieved legendary status amongst mathematicians, because, in the 17th century, the French civil servant and amateur mathematician Pierre de Fermat, one of the greatest figures in the history of Number Theory, had scribbled in the margin of a book that he had a wonderful proof of the theorem, but the margin was too small for him to write it down. The book was a 17th century edition of the classic Greek text on Number Theory written in the first century A.D., Diophantus’ Arithmetica. Fermat subsequently died, leaving mathematicians to search for 350 years for a proof of the theorem.
The hardest problem in all of mathematics?
 Ulam’s Prime number spiral
Ulam’s Prime number spiral
In the 150 years since Riemann’s paper nobody has ever been able to prove or disprove his conjecture, but Fermat’s Last Theorem was finally proved by Andrew Wiles in 1994. The Riemann Hypothesis is now the most famous outstanding problem in mathematics. But the Riemann Hypothesis has far more important consequences for mathematics than Fermat’s Last Theorem. In fact, there are areas of mathematics that have been developed by mathematicians on the assumption that the Riemann Hypothesis is true. The Riemann Hypothesis also appears to be an even more difficult problem than Fermat’s Last Theorem.
Any implicit regularity in the primes that is encoded in the zeta function has still not been explicitly deciphered. However, there is a much simpler pattern exhibited in the distribution of primes. In 1963 the Polish mathematician Stanislaw Ulam, who worked on the American nuclear programme, the Manhattan Project, during the Second World War was doodling abstractedly in the interval between two seminars at a conference. He drew a grid of squares, then he wrote the number 1 at the centre of the grid and continued to write out the sequence of all the positive integers in ascending order spiralling out from the centre. Ulam noticed to his great surprise that when the integers were organised in this way, there was a tendency for the primes to be lined up along diagonal lines in the grid. The result was so unexpected that a picture of the Prime Number Spiral was featured on the cover of the March 1964 issue of Scientific American which included an article by Martin Gardner about the spiral: “Mathematical Recreations: The Remarkable Lore of the Prime Number.” Sci. Amer. 210, 120-128, March 1964.
 Primes along the diagonal of a spiral
Primes along the diagonal of a spiral
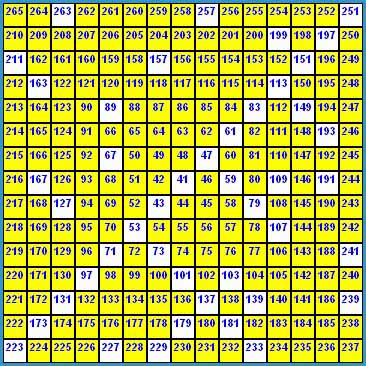
The picture above shows the spiral for the first 100,000 integers. The composite numbers are shown as black dots and the primes are shown as white dots. In the grid numerous long diagonal white lines can clearly be seen. If numbers other than 1 are taken as the starting number of the spiral, the general appearance of the grid is the same. No-one has come up with a clear explanation of why this should be the case. But it implies that there are long sequences of primes that can be generated by formulae such as f(n)=an2+bn+c, where a, b and c are integers.
If we start with the number 41 at the centre of the spiral, we find that the numbers on the diagonal form the sequence f(n)=n2–n+41, which is the formula discovered by Euler that takes prime values for all integer values of n up to 40.
In the illustration the number 41 is situated at the centre and the numbers continue in an anti-clockwise spiral. The squares of the grid that contain composite numbers are coloured yellow and the squares that contain primes are coloured white. The first 15 numbers generated by the formula f(n)=n2–n+41 appear along one of the main diagonals of the square.
 A whirlpool of numbers
A whirlpool of numbers
Although Stanislaw Ulam is generally credited with the discovery of the Prime Number Spiral, it appears that Ulam might not have been the first person to make this discovery. Chapter 6 of Arthur C. Clarke’s classic 1956 novel “The City and the Stars” opens with the hero Jeserac analysing a “whirlpool” of integers on his computer monitor and seeing the primes strung out “across its surface as beads might be arranged at the intersections of a mesh”. It looks as though Arthur C. Clarke had already discovered the Prime Number Spiral seven years before it was found by Ulam. I recently asked Sir Arthur C. Clarke about the inspiration for his discussion of the primes in “The City and the Stars”. He told me that
After half a century I have no idea what made me think of this. I never had a computer until 1970 when H.P. gave me HAL Jr (HP9001), the direct ancestor of the palmtop. But I was impressed by the unfinished Babbage machine, which I must have seen in the Science Museum soon after I moved to London in 1936.
Mathematicians study the properties of primes for their own intrinsic interest. But prime numbers also have modern scientific applications, especially in cryptography. The United States Government Intelligence Agency, the NSA, is the world’s biggest employer of pure mathematicians. Whenever you make a transaction on the internet, such as a credit card purchase, the security of the transaction is ensured by the use of public key encryption using a method based on some subtle Number Theory devised by Ron Rivest, Adi Shamir and Len Adleman, also known as RSA. RSA encryption utilises a numerical key that is formed by multiplying together two very large primes. The security of the system is dependent on the difficulty of factorizing very large numbers. The number of steps that are necessary to factorize a large number using all known algorithms increases exponentially with the size of the number. This means that the cryptographer can always stay one step ahead of the computer. If computer processors become fast enough to factorize the 128 digit numbers that are used for encipherment, we can start to use 512 digit numbers. However, if a mathematician were to find a new more efficient factorization algorithm the security of our enciphered transactions might be under threat. Cryptographers feel safe, because, although leading mathematicians have searched for such an algorithm for many centuries none has ever been found.
Last year three Indian mathematicians – Prof. Manindra Agrawal and two of his graduate students, Neeraj Kayal and Nitin Saxena – published an algorithm for testing whether a number is prime or composite (see Prime time from Issue 22 of Plus). The algorithm employs quite elementary arithmetic and is stated by the authors in just 13 lines. The important new feature of the algorithm is that the time taken to test the primality of a number N increases polynomially with the size of N rather than exponentially. In fact, it increases as the twelfth power of N. Following this revelation, perhaps we shouldn’t be too hasty to rule out the possibility that there is also a simple algorithm for factorization that has similarly been overlooked. Maybe cryptographers should be worried.
http://plus.maths.org/content/whirlpool-numbers